Clausius’ Equivalence of Transformations — Part II — Carnot Cycle
Carnot Cycle demonstrates the equality of the transformations
In a prior blog, it was established how Clausius defined an equivalent set of transformations across a cycle. The equivalence is based on the supposition that each transformation is equal to dQ/dT; and that certain transformation types have the same impact.
Specifically, he states that there are two types of transformations.
- Conversion of heat to work (and conversely, conversion of work to heat)
- Transit of heat from a hot reservoir to a cold reservoir
and that the sum of all these transformations across a cycle is either zero, for reversible cycles, or greater than 0, for irreversible cycles.
Diagram of general thermodynamic cycle showing transformations

Carnot Cycle
The respective transformations can be calculated for a Carnot cycle and can be shown to be equal to each other in the way Clausius supposed.
Diagram of PV diagram of Carnot cycle
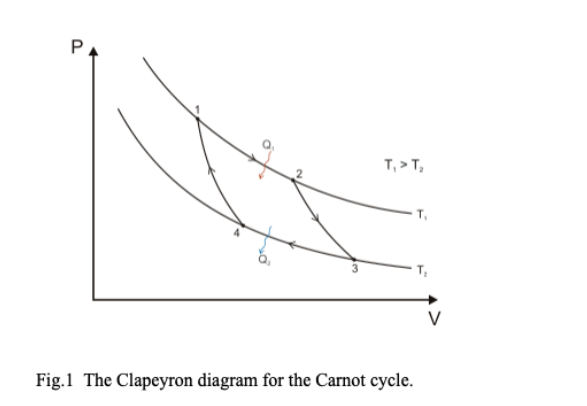
Isothermal Legs
The isothermal legs can be analyzed using the 1st Law:
- dU = dQ — dW
Since these are isotherms, dU=0; hence
- dQ = dW
- dW=pdV
If we assume an ideal gas, the relation for KE for an Ideal gas can be used
- PV=nRT
- dW = (nRT/V)dV
Integrating yields the following expression for the work performed between any two volumes
- W=nRT*ln(Vf/Vi)
But this is now also the heat that is absorbed from points 1 and 2 or the heat expelled between points 3 and 4.
- Qh=nRTh*ln(V2/V1) Heat absorbed in the top isotherm
- Qc=nRTc*ln(V4/V3) Heat expelled in the bottom isotherm
These two quantities can now be modified into the form associated with the ‘transformation’:
- Qh/Th= nR*ln(V2/V1) <<== impact of transformation 1
- Qc/Tc = nR*ln(V4/V3) <<== impact of transformation 2
The question is — are these two quantities the same?
In this case, it’s straightforward to demonstrate that they have the same absolute values but are of opposite signs.
Adiabatic Legs
The adiabatic legs, by definition, do not receive or expel any heat. Hence, from the 1st law, one has
- dU = dQ — dW
- dQ=0, since dT=0
Hence,
- dU = -dW=-pdV
Using the assumption that, for an ideal gas, the change in internal energy is only dependent on temperature (e.g. independent of volume), one has
- dU=n*Cv*dT
Using the Ideal Gas law yields
- -dW=-pdV=-(nRT/V)*dV
Hence,
- dU = -dW
yields
- Cv*dT/T = -R*dV/V
Using that R=Cp-Cv
- Cv*dT/T = -(Cp-Cv)*dV/V
- Cv*dT/T + (Cp-Cv)*dV/V = 0
- dT/T + [(Cp-Cv)/Cv]*dV/V = 0
- dT/T + [gamma-1]*dV/V = 0
- gamma=Cp/Cv — 1
Integrating yields
- ln(T) + A1 + ln(V)^[gamma-1]+B1=C1
Re-ordering
- Ln (T * (V)^[gamma-1] )= Constant
- T*V^[gamma-1]= Constant
Performing the integrals on each adiabatic leg in turn yields
- ln(Tc/Th) +[gamma-1]ln(V3/V2) = C <<<== from 2 to 3
- ln(Tc/Th) +[gamma-1]ln(V4/V1) = C <<<== from 1 to 4
Which can be reduced to
- Ln [ (Tc/Th)*(V3/V2)^[gamma-1] ] = C
- Ln [ (Tc/Th)*(V4/V1)^[gamma-1] ] = C
Equating
- Ln [ (Tc/Th)*(V3/V2)^[gamma-1] ] = C = Ln [ (Tc/Th)*(V4/V1)^[gamma-1] ]
Hence,
- V3/V2 = V4/V1
or
- V3/V4 = V2/V1
Equality of Transformations
From the first section, the impact of each transformation was determined to be
- Qh/Th= nR*ln(V2/V1) <<== impact of transformation 1
- Qc/Tc = nR*ln(V4/V3) <<== impact of transformation 2
Since the volumes are related per
- V3/V4 = V2/V1
The impact of the transformations is indeed now demonstrated to be equal in magnitude and opposite in sign:
- Qh/Th = nR*ln(V2/V1) = — Qc/Tc = — nR*ln(V3/V4)
- Qh/Th + Qc/Tc = 0
The entropy lost by heat escaping the hot bath at T=Th is exactly counterbalanced by the entropy gained by the heat escaping into the cold bath at T=Tc.
The net entropy change across the cycle is in this case — zero.
Remarkably, a quantity, known as entropy, is conserved across the cycle.
More Discussion
Clausius’ transformations can be better understood when viewed from an energy perspective. See Clausius’ Equivalence of Transformations — Part III — Energy Viewpoint